Section 4.6 is entitled “Variation of Parameters.”
We’ve seen this method in the past, except we used it only
for first-order differential equations. In this section, we’re interested in
solving the equation y” + p(t)y’ + q(t)y = g(t). Notice that p and q are
functions of t, instead of restricting them to be constants.
If we first look at the homogeneous equation y” + p(t)y’ +
q(t)y = 0, then the general solution to that equation would be yh =
C1y1 + C2y2. As usual, C1
and C2 are arbitrary constants.
Like our previous process, the method of variation of
parameters makes us think of C1 and C2 are unknown
functions v1(t) and v2(t). Then we’ll look for a
particular solution to our original inhomogeneous equation, in which our
particular solution will have the form yp = v1y1
+ v2y2. In other words, we have a lot of similarity
between this method of variation of parameters and our previous one we used to
solved linear equations back in Chapter 2 (i.e. http://differentialequationsjourney.blogspot.com/2013/09/super-serious-and-not-so-funny-linear.html).
When we compute the derivative of yp,
What we have in the brackets, we will set
equal to zero.
Differentiating again, we get
When we plug yp, yp’
and yp” into our original inhomogeneous equation y” + p(t)y’ + q(t)y
= g(t), we get
Since we defined y1 and y2
to be solutions to the homogeneous equation, this simplifies to be
In other words, yp will be a
solution to our original inhomogeneous equation provided that
At this point, we have two equations for
v1 and v2, which are
Since this is a system of linear
equations, we can observe that our coefficient matrix would be
This means that this system can be solved
provided that the determinant of this matrix is nonzero. Something to observe
about the determinant is that is also the Wronskian of y1 and y2.
Since y1 and y2
form a fundamental set of solutions for our equation, this means they are
linearly independent and that means the Wronskian will be nonzero. Hooray!
Back to our system of equations for v1
and v2: We can solve these equations to obtain
Something to note about these two
equations is that the denominators will always be nonzero since they are both
the Wronskian. Double hooray!
When we integrate these equations, we get
Now we’ll have a particular solution once
we plug these back into yp = v1y1 + v2y2.
And now you have a method to solve
inhomogeneous differential equations of higher orders! Of course, this method
requires for you to first find a fundamental set of solutions to the
homogeneous equations, and also to be able to compute those scary-looking
integrals for v1 and v2, but this method is still
important.
That’s it for 4.6! I’ll see you in 4.7!





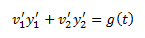


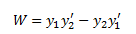

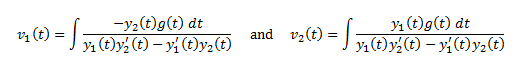
No comments:
Post a Comment