Section 8.2 is entitled “Geometric Representation of
Solutions.”
The model we’re going to use this section is called the
Lotka-Volterra model of predator-prey populations. I’m not going to derive it;
rather, I’ll hand you the final system and you can take my word that it’s all
correct:
This model is nonlinear and autonomous.
One way you can represent this model is to plot all of the
components of the solution. You can probably Google it (or go here http://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equation
or here http://mathworld.wolfram.com/Lotka-VolterraEquations.html)
but the graphs seem to be a periodic variation of the populations of predators
and prey.
Another way we can see the solution is to look at a
parametric plot. Let’s set u(t) =
(F(t), S(t))T and plot t → u(t)
= (F(t), S(t))T. This view would be in R2, so we can call this solution curve a phase plane.
To see the phase plane of the Lotka-Volterra model, you can
go here: http://mathinsight.org/applet/lotka_volterra_phase_plane_versus_time_population_display
For those of you who are too lazy to click on the link (or
copy-paste), it looks like an egg. More specifically, it shows how the two
populations interact. A fancy term for “egg” is “closed curve”, which means it
tracks over itself as time increases. This makes sense, if we are to believe
that the solution is indeed periodic. The derivative u’(t) is a vector tangent to our egg at a point u0 = u(t0).
This kind of analysis can be done for higher dimensions, (t →
y(t) is the parameterization for a
curve in Rn, and y’(t) is a vector tangent to the curve
at y(t)). It’s just much harder to
visualize once you go into dimensions higher than 3.
Now let’s suppose we have a planar system:
In this case, y(t)
= (y1(t), y2(t))T would be a solution. We
could look at the solution curve t → y(t)
in the plane. In this case, this y1y2 plane is still
called the phase plane, but solution curve is called the phase plane plot or
solution curve in the phase plane.
Generally, we’ll be in dimension n and our equation will
have the form x’ = f(t, x). The x-coordinates
would be called the phase space, and the plot of the curve t → x(t) is called the phase space plot. They’re
pretty important for autonomous systems.
Let’s consider the autonomous system
Note this is autonomous because the independent variable
doesn’t appear explicitly on the right-hand side. Let’s assume that f and g are
defined in a rectangle R in the xy-plane. Let’s consider the solution of the
form (x(t), y(t)) and the curve t → (x(t), y(t)) in the xy-plane. This means
there will be a vector
that will be tangent to this curve. So if we assign a vector
to each point in our rectangle R, then we would have what is called a vector
field of our original system. For a pretty picture of the Lotka-Volterra vector
field, you can go here http://mathforum.org/mathimages/index.php/Field:Dynamic_Systems#Maps
If we picked a starting point, then the vector field would
show us how that curve would form and what our egg would look like. Ultimately,
the curve goes back to our original point, which makes sense since we have an
egg and not a bowl (or some equivalent open-ended egg shape).
Now let’s start with the general system
Now f and g are defined in a three dimensional shoebox R.
This would be in the (t, x, y) space. The limits on this space, in a more
general form, would be
In this case, the vector field would be (f(t, x, y), g(t, x,
y)), which means it now depends on t, x, and y. Well, if t can change as well,
then it doesn’t make much sense to observe a vector field in the phase plane.
In this case, we will be looking at a three dimensional direction field.
We’re going to consider the curve parameterized by t → (t,
x(t), y(t)) in our shoebox R. This time, our tangent vectors will take the form
Something interesting to note about this is that the vector
(1, f(t, x, y), g(t, x, y)) can be computed without knowing the solution of the
system. This type of interpretation of our system will be called (surprise,
surprise) a direction field.
The solution to the Lotka-Volterra model in a
three-dimensional direction field looks really awesome. While my skim of the
internet didn’t produce a website that could accurately depict this phenomenon,
I encourage you all who have a copy of the book to take a look (page 344).
Since we discussed three different ways to visualize
solutions, you can put them all together in a composite graph.
There’s no best way to visualize one of these solutions. The
book encourages you to look at all of the visualizations. I encourage you to
get correct answers and pass tests (and understand how to visualize these
things).
Finally, a thing from the book concerning higher dimensions:
“What do we do in higher dimensions? What we do not do is become daunted by the
seeming impossibility of visualizing in dimensions greater than 3. Instead we
try anything that that seems like it will be helpful” (345).
Don’t be daunted, my friends. I’ll see you when I see you.




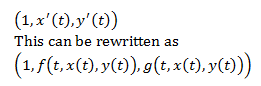
No comments:
Post a Comment