Section 4.3 is entitled “Linear, Homogeneous Equations with
Constants Coefficients.”
These are equations of the form y” + py’ + qy = 0. In this
case, p and q are constants. First, we’re going to look at the first-order
equation y’ + py = 0. This is an exponential equation, in which its general
solution is y(t) = Ce-pt. In this case, C is just a constant. We’re
going to look for a solution of the type y(t) = eλt, where λ is a
constant. When you put this type of solution into the original differential
equation,
 |
| So Word apparently doesn't like λt... |
That final equation is called the
characteristic equation for our original second-order differential equation. The
polynomial is called the characteristic polynomial, and the roots of this
equation are called characteristic roots. Then if λ is a characteristic root,
then y = eλt is a solution to the differential equation.
If you write both the differential
equation and the characteristic equation together, then
They look very similar.
The roots for the characteristic polynomial
are given by the quadratic formula:
When you look at the discriminant (p2
– 4q), there are three cases to consider:
1. Two real roots (p2 – 4q
> 0)
2. Two complex roots (p2 – 4q
< 0)
3. One repeated real root if p2
– 4q = 0
For the three cases (and the summary), I
have a lot of quotes for you. I was doing so well without direct quotes! Oh
well…such is life, I suppose.
For two real roots: “If the
characteristic equation λ2 + pλ + q = 0 has two distinct real roots
λ1 and λ2, then the general solution to y” + py’ + qy = 0
is
where C1 + C2 are
arbitrary constants” (151).
For the complex roots, whenever there’s a
variable with strikethrough (like this) and it’s also surrounded by
brackets, I changed it from an overstrike (which I can’t show in the regular
words because overstrikes are hard) to a strikethrough. I thought I’d let you
know before you started to wonder why I have brackets around strikethrough
stuff.
For two complex roots: “Suppose the
characteristic equation λ2 + pλ + q = 0 has two complex conjugate
roots, λ = a + ib and [λ] = a – ib.
1. The functions
form a complex-valued fundamental set of
solutions, so the general solution is
where C1 and C2 are
arbitrary constants.
2. The functions
form a real-valued fundamental set of
solutions, so the general solution is
where A1 and A2 are
constants” (153).
For our third case, with the repeated
roots: “If the characteristic equation λ2 + pλ + q = 0 has only one
double root λ1, then the general solution to y” + py’ + qy = 0 is
where C1 and C2 are
arbitrary constants” (155).
And finally, the summary of all of this (put in bold and italics because summaries):
“If p2 – 4q > 0, the
characteristic equation has two distinct, real roots λ1 and λ2.
A fundamental set of solutions is
If p2 – 4q = 0, the
characteristic equation has one repeated real root λ. A fundamental set of
solutions is
If p2 – 4q < 0, the
characteristic equation has two complex conjugate roots a ± ib. A fundamental
set of solutions is…” (156).
And that’s it for 4.3! I seriously can’t
believe I got this done tonight. I’m super excited about this. I don’t have to
do this section tomorrow! Hooray!
Enjoy all of the quotes. Also enjoy the
beginnings of our journey through Chapter 4.
I shall see you in 4.4! :D




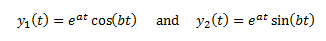

No comments:
Post a Comment