Chapter 8 is entitled “An Introduction to Systems.”
Section 8.1 is entitled “Definitions and Examples.”
I’m going to make the observation here and now that any
[chapter].1 section will be entirely dedicated to exposition for the succeeding
sections.
In other words, [chapter].1 summaries will be particularly
dull. I try my best (considering the people who pretend to read/care/enjoy this
blog are not emotionally attached to the blog or the class whatsoever, besides
my teacher, of course) but for the most part, I don’t have a lot of math
jokes/puns to throw at you. Instead, I have math numbers and math words.
Anyway, ready for chapter 8? And the five sections the
weekly schedule says we’re covering?
Let’s start off this summary with talking about sick people.
Let’s say there’s a population of people, N. There’s also
there’s this disease that’s going around. We have three assumptions about this
disease:
1. The disease lasts a short amount of time and doesn’t kill
people (not often, anyway).
2. The disease spreads through physical contact.
3. After someone recovers from the disease, he/she will be
immune.
Knowing these things, we can split our population N into
three groups: people who have never had the disease, people who currently have
the disease, and people who have recovered from the disease. We’ll call the
first group the susceptible, S(t); the second group will be called the
infected, I(t); the third group will be called the recovered, R(t). This means
N = S + I + R.
Our first assumption means we can ignore births and deaths.
This is nice because N is then constant. Let’s also think about how S(t) will
change; susceptible people will catch the disease from infected people and then
change groups. This means the rate of change for these two groups is
proportional to the number of contacts made. The number of contacts will then
be proportional to the product SI of the two populations. This will take the
form
In this case, a is a positive constant.
Thinking about how I(t) will change, we
think about two different ways. Susceptible people get sick, and infected
people get better. We figured out the “susceptible people get sick” part, with
our product above. With the “infected people get better part,” this means there
will be a rate of recoveries (with some positive constant b). Thus the form
will be
Thinking about how R(t) will change,
infected people will get better. Thus we already have the form for the rate of
change of R:
If we want to wrap everything up in a
nice bow, we’ll have
This is called the SIR model. Notice it
is nonlinear and autonomous.
The last equation isn’t really needed.
The first two equations form a planar and autonomous system. We’ll get the
system
This is also referred to as the SIR
model.
Notice the SIR model only involves
first-order derivatives of the system. It is called a first-order system. Thus
we can conclude the order of a system is determined by the highest order
derivative in that system. Generally, a first-order system of two equations
will have the form
In this case, f and g are functions. A
solution to this system would have the form
As always, this will be on some interval
of t.
The number of equations should always be
equal to the number of unknowns. This will be called the dimension of the
system. Thus the system above has dimension 2, and a general system of n
equations with n unknowns will have dimension n. A dimension 2 system will be
called a planar system.
Notice that our first form of the SIR
model is dimension 3, but the second form is a planar system.
If we have a general system
We can write this system in terms of
vectors. We can set
One last thing for this section: “…there
is a system of first-order equations that is equivalent to any system of
higher-order equations, in the sense that a solution to one leads easily to a solution
to the other” (335). This means that any application that involves higher-order
equations will have an equivalent model with a first-order system. This is nice
for the book because we can spend a lot more time studying first-order
equations. This is also nice because numerical solvers (remember the two
sections from chapter 6?) are more geared toward first-order equations.
Here’s an example of how you can find the
first-order system of an equation:
Let’s rename the variables:
So if x solves our original equation,
this means that our sets of u functions will solve our new system.
All right, that’s it for section 8.1!
Section 8.2 seems a little more yucky than this one, but I’m sure we’ll get by
just fine.
I’ll see you when I see you.







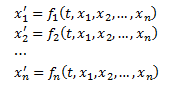


No comments:
Post a Comment