Section 9.6 is entitled “The Exponential of a Matrix.”
Allow me to warn you up front that this section is chock-full of propositions and theorems and such nonsense, so be aware quite a bit of this
summary will be quotes. I apologize only because summaries should be more of an
“in your own words” kind of thing, and that’s not the case sometimes. However,
I hesitate to apologize only because the authors are paid money to explain math
things the best, and I am not paid to write this blog. Therefore, I think I’m
allowed to use direct quotes now and then.
Let’s now discuss what we do when we have an eigenvalue
where the geometric multiplicity does not equal the algebraic multiplicity.
When n = 1, we have an initial value problem
From there, we looked for exponential
solutions to the system x’ = Ax of the form x(t) = eλtv.
This worked as long as λ was an eigenvalue of A and v was the associated eigenvector. Most of the time, this has worked
beautifully and we’re happy and can move on with our lives. However, we have
moments and examples where this doesn’t work out and we’re not happy anymore. So
our goal is to find a term called the exponential of a matrix, which will give
us solutions to the equation x’ = Ax.
In order to define the exponential of a
matrix, we actually have to look at the series for the exponential function
(which I had to look at for my physics homework last week, so I’m really
exciting and I’m kind of geeking out about it. Don’t judge me. No but seriously I'm really excited about this). Therefore, the
exponential of the matrix A is defined to be
Just for clarification, A2 =
A*A, A3 = A*A*A, etc. Also, we have I as the first term because A0
is I. Since A is defined to be an n × n matrix, eA will also be an n
× n matrix (provided this series converges). Since we’re dealing with a series,
we must consider the partial sum matrices
The book says that series in the
definition (i.e. the infinite series I’ve shown you) will converge for every
matrix A. They don’t prove it, and I don’t want to prove it, so I guess we’ll
all have to take their word for it.
Here are some fun facts from the book:
“The exponential of a diagonal matrix is the diagonal matrix containing the
exponentials of the diagonal entries. In particular, we have
When r = 0, we have the important special
case
Unfortunately,
there is no easy formula for the exponential of a matrix that is not diagonal”
(417).
Well, that last fact wasn’t fun at all,
was it?
So here’s a proposition for you: “Suppose
A is an n × n matrix.
1. Then
2. If v ∈ Rn, the
function x(t) = etAv is a solution to the initial value
problem x’ = Ax with x(0) = v” (418).
In other words, we’ll be able to solve the
initial value problem if we can compute etAv.
Since we’re dealing with a sum, we could
potentially have a finite sum very easily if a majority of the terms turn out
to be 0. This leads us to the next
proposition for an n × n matrix A:
“1. If Av
= 0, then etAv = v for all t.
2. If A2v = 0, then etAv = v + tAv for all t.
3. More generally, if Akv = 0, then
for all t” (419).
This property is called truncation (as in the
infinite sum is truncated to a finite sum). This means we can compute etAv when v is in the nullspace of A (or in the nullspace of a power of A).
If we look at the properties of these
exponentials, we’ll see we get one of them from a law of exponents, mainly that
ea+b = eaeb. However, this isn’t the case for
every pair of matrices (let’s call them A and B).
Since we learned in day one of matrices that
it’s rarely true for AB = BA (in math words, we would say that A and B commute).
However, I do not fear for the future, since this is a textbook and the authors
are most likely paid money to find examples that work.
Another property of these exponentials we’ll
be looking at is one to do with singularity, namely “if A is an n × n matrix,
then eA is a nonsingular matrix whose inverse is e-A”
(420).
Another proposition for you: “Suppose A is an
n × n matrix, λ is a number, and v
is an n-vector.
1. If [A – λI]v = 0, then etAv = eλtv for all t.
2. If [A – λI]2v = 0, then eλt(v + t[A – λI]v) for all t.
3. More generally, if k is a positive integer
and [A – λI]kv = 0, then
for all t” (421).
Recall that [A – λI]v = 0 if and only if λ
is an eigenvalue and v is the
associated eigenvector. The solution in this case would be y(t) = etAv =
eλtv which agrees what we
learned previously in the chapter. Hooray consistency!
A definition: “If λ is an eigenvector of A,
and [A – λI]pv = 0 for some integer p ≥ 1, we will call v a generalized eigenvector” (422).
And now for a theorem: “Suppose λ is an
eigenvector of A with algebraic multiplicity q. Then there is an integer p ≤ q
such that the dimension of the nullspace of [A – λI]p is equal to q”
(422).
So you may be wondering why λ is now an
eigenvector. Well, I have no idea, because I originally thought it was a typo.
Well, they either made the same typo in two different places, or they meant to
make λ an eigenvector. I don’t know.
In any event, we now have a procedure for
solving linear systems.
“1. Find the smallest integer p such that the
nullspace of [A – λI]p has dimension q.
2. Find a basis for {v1, v2,…,
vq} of the nullspace of
[A – λI]p.
3. For each vj, 1 ≤ j ≤ q, we have the solution…” (423).
Well, that’s all the learning for section 9.6!
I’m not online right now so once I get online I’ll definitely look for websites
with examples. I feel like general infinite sums only go so far before you need
to know how to deal with them when you enter the real world of dealing with
examples. There are probably tons of examples out there, so I’m not worried.
EDIT: I found a couple of websites, some not
really related to this section, which might help you out with eigenvalues and
eigenvectors and such.
More of an overview: http://tutorial.math.lamar.edu/Classes/DE/SystemsDE.aspx
and http://www.sosmath.com/diffeq/system/linear/eigenvalue/eigenvalue.html
Real eigenvalues: http://tutorial.math.lamar.edu/Classes/DE/RealEigenvalues.aspx
and http://www.sosmath.com/diffeq/system/linear/eigenvalue/real/real.html
Complex eigenvalues: http://www.sosmath.com/diffeq/system/linear/eigenvalue/complex/complex.html
Matrix exponential stuff: http://www.sosmath.com/matrix/expo/expo.html
and http://faculty.atu.edu/mfinan/4243/section611.pdf
and http://www.math.wisc.edu/~dummit/docs/diffeq_3_systems_of_linear_diffeq.pdf
(starts at the very bottom of the eighth page)
In any event, I’ll see you in 9.7.
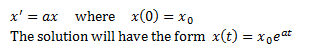

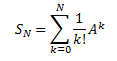
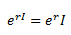
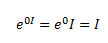





No comments:
Post a Comment