Section 8.4 is entitled “Linear Systems.”
Let’s start with what the book means by linear systems. Kind
of like linear equations (and by “kind of like” I mean “exactly like”), if
there are no products, powers, or higher-order functions, then the functions in a
system will appear linearly. This means that a system where the functions
appear linearly will be called a linear system.
For example, the following systems are linear:
The following systems are not linear:
Putting things into a more general form,
a linear system will have the form
The functions x1 through xn
are considered to be unknown functions. Known functions are the coefficients aij(t)
and fi(t), and are strictly functions of the independent variable.
They are defined for all t in a region I = (a, b), which would be an interval
in R.
This form is said to be in standard form.
Something to note is that there are n unknown functions and n equations; this
would make the system’s dimension n. If fi(t) is zero (for all fi),
then the system is homogeneous. If the fi(t)s are nonzero, then the
system is inhomogeneous. Thus the fi(t)s
will be called the inhomogeneous parts, or the forcing term. (It’s called a
forcing term since, in applications, it arises from external forces.)
The matrix notation for linear systems is
as follows:
We can compact all this information in
the equation x’(t) = A(t)x(t) + f(t), or x’ = Ax + f.
The three applications of linear systems
that are presented in the book are springs (more than one, since this is a
linear system), electrical circuits,
and mixing problems.
Since this is a summary and all, I could
leave it at that, but since I’m a physics major, I’m going to show you
electrical circuits. Also, I have a test in this class next week (if you’ve
been keeping up, I have a test in differential equations as well. Next week is
not going to be a bucket of fun) and the practice could come in handy.
Before I jump on that train of fun times,
here are some websites detailing the other two examples.
Springs: http://en.wikipedia.org/wiki/Spring_system
and http://www.sosmath.com/diffeq/system/linear/basicdef/basicdef.html
Mixing problems (examples): http://stevesweeney.pbworks.com/f/MPM2D+-+Linear+Systems+07+-+Mixture+Problems+-+W2011.pdf
and http://www.purplemath.com/modules/mixture.htm
Here’s a handy recreation of a circuit
from the book:
First we use Kirchhoff’s current law to
get that I = I1 + I2. These are labeled on the diagram by the blue arrows and the I (1) and I (2).
Kirchhoff’s voltage law tells us
that
This is for the loop that contains the
voltage source, the resistor, and the inductor. I also reminded you of the physics. (Sometimes I feel like I'm obligated. Sometimes I just don't care if you want physics shoved down your throat or not.) Anyway, when we continue on with our analysis,
For the loop that contains the voltage
source, the resistor, and the capacitor, Kirchhoff’s Law tells us
This forms an inhomogeneous and linear
system
Finally, to write this
system in matrix notation, we’ll have
This system can also be written as I’ = AI + F.
All right, that’s it for section 8.4. I
had to write up the last part of this section twice because Microsoft Word is
an absolutely perfect and flawless program that will always save my documents
in the way I want them to be saved.
I hope to get 8.5 up by tomorrow or
Sunday. I also hope to get a review blog post/some sort of note/cheat sheet
type of blog post up here too. We’ll see what happens on that, though.
I’ll see you when I see you.








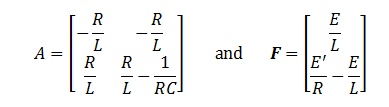
No comments:
Post a Comment