Section 4.7 is entitled “Forced Harmonic Motion.”
So back in section 4.4 (http://differentialequationsjourney.blogspot.com/2013/10/44-lets-talk-physics-er-harmonic-motion.html)
we derived the model for harmonic motion:
We’re first going to deal with forced undamped harmonic motion, where c = 0:
We need to consider two cases when
dealing with undamped harmonic motion: when the driving frequency ω
is equal to the natural frequency and when it is not.
Case
one: the driving frequency is not equal to the natural frequency
We use the method of undetermined
coefficients to find the solution to this. I’m going to briefly summarize it.
We start by looking for a particular
solution of the form
In this case, a and b are the
undetermined coefficients. We substitute this particular solution into our
inhomogeneous equation for undamped harmonic motion (i.e. the inhomogeneous
harmonic motion model where c = 0), and we find what a and b are equal to.
This gives us our particular solution, and now we can create our general
solution x(t) = xh(t) + xp(t).
If we look at the solution where the
motion starts at equilibrium, then we have the initial conditions x(0) = 0,
x’(0) = 0.
Just as an example, here’s what forced
and undamped harmonic motion looks like. This also shows what the book calls beats, which occur whenever two
frequencies that are very similar interfere with each other. In order to
understand beats, let’s introduce a couple of new things:
This then leads us to the equation
So then we have what’s called an
envelope, where there’s a slow oscillating amplitude and a faster oscillation.
 |
| (Wikipedia) |
The example I have is not for the
cos(11t) – cos(12t) business. It’s just to illustrate what an envelope looks
like. The actual envelope is the red dotted line. It's through the maxima of the faster oscillation (in blue).
Case
two: driving frequency equals natural frequency.
Now we look for a particular solution of
the form
Again, we insert this into the
inhomogeneous equation for undamped harmonic equation, find a and b, and then our particular solution would be
We have a special case where x(0) = C1
= 0, x’(0) = C2 = 0. In this next picture, A = 8 and ω0
= 4.
This type of behavior is called resonance.
Now, let’s add a damping term to the
system. We’re now dealing with the equation
Suppose we’re dealing with an underdamped
case, where c < ω0. Back in section 4.4 we found
that the general solution is
In order to find a solution to the
inhomogeneous equation, we once again use the method of undetermined
coefficients, but it’s easier to use the complex method. We’re now looking for
the solution z(t) = aeiωt to the equation
We substitute out z(t) into that equation,
we’ll get
We then get
The function H is called the transfer
equation.
Looking back at P for a second, we see that
We want to write this in polar form, so we’ll
need a positive number R and an angle φ such that
So then we can write the transfer function as
We now can see that the solution to our complex
equation is
The homogeneous part of our general solution
has the factor e-ct which is called the transient term because it quickly decays to 0 as t goes to
infinity. After a factor Tc = 1/c, this factor decreases to e-1
and the amplitude has decreased to e-1 times its original size. Tc
is called the time constant. Because
xp does not decay, it is called the steady-state. This term is driven by the external force Acos(ωt).
Finally, let’s discuss lumping parameters. We do this in order to see how the gain G
depends on ω while we study the steady-state term.
This is still complicated, but this expression
for gain is much easier to understand than before. Because the natural
frequency is fixed, let’s look at
Something to note about this is “…the maximum
gets larger as the damping constant decreases. This is another example of
resonance…the resonance increases as the damping constant decreases” (185).
That’s it for section 4.7 and for chapter 4 as
a whole. We have 7 sections from chapter 5 and possibly some selections from
chapter 10. In any event, we’re close, my friends.
I’ll see you in chapter 5.





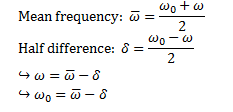




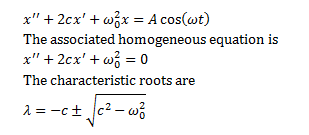


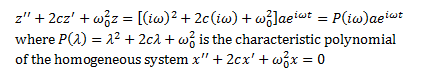






No comments:
Post a Comment