Section 5.7 is entitled “Convolutions.”
Let’s review a little bit of what we have learned in the
past:
(It’s probably near the end of this epic mashup: http://differentialequationsjourney.blogspot.com/2013/11/52-54-where-you-refine-your-powers-of.html)
At the end of our summary through 5.6 (i.e. http://differentialequationsjourney.blogspot.com/2013/11/56-last-second-to-last-section-maybe.html)
we talked about something called the unit
impulse response function. Since the denominator of our Laplace transform
is the characteristic polynomial of our second order differential equation, we
can rewrite that Laplace transform as
In this case, E(s) is the Laplace transform of the unit
impulse response function e(t) for our differential equation. So now we can
find a solution to the differential equation by taking the inverse Laplace
transform of our rewritten Laplace transform, i.e.
Let’s now look at a proposition:
“Suppose that f
and g are functions of exponential
order. Suppose that ℒ(f)(s) = F(s) and ℒ(g)(s) = G(s). Then
Note that the choice of the variable of u is merely a
choice. The variable of integration could be anything, in theory, since the
resulting expression is a function of t at the end of the day.
Now, let’s define something:
“The convolution of two piecewise
continuous functions f and g is the function f * g defined by
The means we can rewrite what we said in the proposition as
Now, let’s look at a theorem:
“Suppose f and g are functions of exponential order.
Then
Here’s another theorem:
“Suppose f, g, and h are piecewise continuous functions. Then
1. f * g = g * f
2. f * (g + h) = f * g + f * h
3. (f * g) * h = f * (g * h)
4. f * 0 = 0” (235).
(Note: three theorems separate us from the end of this
blog.)
Now, we want to think in terms of the general solution to
our original initial value problem (which I’ll state once again because why not
and also because we’re going to make it a little more general):
Let’s take a look at the theorem that will answer all our
questions:
“The solution to the initial value problem [above] can be
written as
[where ys(t) is the state-free solution and yi(t)
is the input-free solution]. If e(t) is the unit impulse response function for
the system, then the state-free response is
and the input-free response is
Let’s now think of properties of the convolution. For one
thing, f * 1 is NOT equal to f. This means, unlike a lot of other subjects in
mathematics, the function 1 is not the identity for the convolution product.
Here’s a theorem for the identity:
“Suppose f is a
piecewise continuous function. Then
Allow me to take the time right now to remind you that δ0
is the delta function when p = 0 (http://differentialequationsjourney.blogspot.com/2013/11/56-last-second-to-last-section-maybe.html).
Something nice about this result is that
Finally (and by finally, I mean for the final time in this blog), here’s a theorem:
“Suppose f and g are piecewise differentiable
functions. Then
Here are some websites concerning the interesting phenomenon
of convolutions:
http://en.wikipedia.org/wiki/Convolution
(This will probably be more confusing than helpful but I’m adding it anyway)
http://faculty.atu.edu/mfinan/4243/section76.pdf
(This contains more problems for you to work out than examples, but that’s
okay, I suppose)
http://www.swarthmore.edu/NatSci/echeeve1/Class/e12/Lectures/ImpulseConvolution/ConvolutionExamples.pdf
(This contains quite a few graphs. There were no graphs in the section in the
book so this might be more confusing than helpful.)
All right, that’s it. My teacher told me to not worry about
chapter 10, so I won’t.
Wow, this is weird. I’m finishing something that has taken
up so much time in my semester. This is bittersweet. I like the idea of not
having to worry about this blog anymore, but I kind of enjoyed it in a
no-one-reads-this-anyway-so-I-don’t-need-to-feel-pressured sort of way.
The journey is over summary-wise but not semester-wise. I
still have a couple of weeks before this semester is over so we’ll see what
happens.
Goodbye, math blog. (For now.)



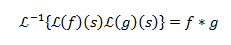




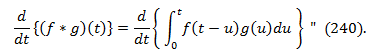
No comments:
Post a Comment