Section 5.6 is entitled “The Delta Function.”
So guys. This is a pretty theorem-heavy section. In fact, I
don’t quite count it as a section I had to summary because all I have to do is
quote all the definitions and theorems and be on my merry way. Sure, it takes
some effort on my part, but it’s a really nice section to end on until at least
Friday (once my test is dead and gone).
Let’s start with a definition of what we mean by the impulse
of a force:
“Suppose F(t) represents a force applied to an object m at
time t. Then the impulse of F over the time interval a ≤ t ≤
is defined as
In physics terms, the impulse is the change in
momentum of a mass as a force is being applied to it during a certain time
interval (in this case, a ≤ t ≤ b). If we recall a simpler time (in chapter 2,
I believe) (http://differentialequationsjourney.blogspot.com/2013/08/section-23-words-and-then-numbers.html)
when we first thought of Newton’s Second Law, we know F = ma = m*dv/dt.
Therefore we can rewrite impulse as
If you know even a little bit about physics,
you’ll recognize the form mv as the function of momentum. Thus impulse really
is the change of momentum on an interval of time.
Now let’s consider a force of unit impulse
over a short interval of time, which is what we’ll recognize as a piecewise
continuous function. We can also translate this into terms of the Heaviside
function:
The interesting thing about this function is
that for any epsilon, there will be an area that is a rectangle (since it’s a
piecewise function that has constants as its functions) and the area of that
rectangle will always be 1. So if we want a model of this kind of force (which
is sharp and instantaneous) as a time t = p, then we can take the limit as ϵ
goes to zero.
Now let’s define something:
“The delta function centered at t = p is
the limit
When p = 0, we will set δ = δ0”
(229).
Something interesting about this function is
that it’s not even a function. Mathematicians call it a generalized function or
a distribution.
Let’s look at two theorems and a corollary:
“Suppose p ≥ 0 is any fixed point and let φ be
any function that is continuous at t = p. Then
In particular, this theorem can be used to
compute the Laplace transform of the delta function centered at p” (230).
“For p ≥ 0, the Laplace transform of δp
is given by
Finally, the case when p = 0 is important (and
slightly obvious), but ℒ(δ0)(s) = 1.
Finally, here’s a definition and a theorem:
“The solution e(t) to the initial value
problem
is called the unit impulse response function
to the system modeled by the differential equation” (230).
“Let e(t) be the unit impulse response function
for the system modeled by the equation
The Laplace transform of e is the reciprocal
of the characteristic polynomial P(s) = as2 + bs + c.
That’s it for 5.6. I kind of wish I wanted to
just finish the chapter and get 5.7 up tonight, but I don’t. I have other
homework I need to get started since I have limited time to study for my test.
Yay obligations!
I’ll see you in 5.7 (in a good while. I hope
you enjoy your break as much as I will enjoy mine).
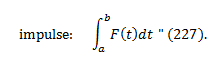



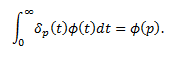


No comments:
Post a Comment