Section 5.2 is
entitled “Basic Properties of the Laplace Transform.”
This section is just a ton of propositions. Seriously, I
could leave the summary at just that and I think everyone would agree that I
have successfully summarized this section.
Oh, well. Onto ALL of the definitions! (Note: Since this is
just a summary blog, I will not be supplying the proofs. I shall be milking the
“it’s just a summary” excuse quite a bit for this section.)
“Suppose y is a piecewise differentiable function of
exponential order. Suppose also that y’ is of exponential order. Then for large
values of s,
where Y(s) is the Laplace transform of y”
(197).
The point of this proposition is that now
it’s relatively easy to find the derivative of a function. Now, you could throw
out really easy functions with really easy derivatives (f(t) = t, f(t) =
sin(t), f(t) = et, etc.) but for other functions, it might be easier
to use this method.
“Suppose that y and y’ are piecewise
differentiable and continuous and that y” is piecewise continuous. Suppose that
all three are of exponential order. Then
where Y(s) is the Laplace transform of y.
More generally, if y and all of its derivatives up to order k-1 are piecewise
differentiable and continuous, and y(k) is piecewise continuous, and
all of them have exponential order, then
“Suppose f and g are piecewise continuous
functions of exponential order, and α
and β
are constants. Then
The point is that the Laplace transform
of a linear combination of functions can be computed by taking the Laplace
transform of each term separately and then adding up the result” (199).
“Suppose f is a piecewise continuous
function of exponential order. Let F(s) be the Laplace transform of f, and let c
be any constant. Then
“Suppose f is a piecewise continuous
function of exponential order, and let F(s) be its Laplace transform. Then
So that’s it for section 5.2. I told you
it was a lot of propositions.
Section
5.3 is entitled “The Inverse Laplace Transform.”
Before we talk about the inverse, we need
to introduce a theorem to clear up any concern.
“Suppose that f and g are continuous
functions and that ℒ(f)(s) = ℒ(g)(s) for s > a. Then f(t) = g(t) for all
t > 0” (203).
In other words, we have yet another uniqueness
theorem to tuck underneath our belts. Also, I couldn’t prove this to you even
if I had the proof in front of me, because apparently the proof goes beyond the
scope of the book. That both terrifies me and excites me (I wouldn’t be a good
physics major if I wasn’t curious about everything, now would I?).
Anyway, onto the definition:
“If f is a continuous function of exponential
order and ℒ(f)(s) = F(s), then we call f the inverse
Laplace transform of F, and write
Here’s a Paint picture to help clear up any
confusion (and also for any visual learners out there):
A proposition for you: “The inverse Laplace
transform is linear. Suppose that ℒ-1(F) = f and ℒ-1(G) =
g. Then for any constants a and b,
Also, here’s a table of some common Laplace
transforms (which you can probably find in a million other places here on the
internet, but here it is nonetheless):
In order to complete this section, I have to
bring back something I am not particularly fond of: partial fractions.
If you want a refresher on the subject (I know
I did), here are a couple of websites for you (personally, I’m not very fond of
the Wikipedia article on the subject. I’d say to go for the one with pretty
colors): http://en.wikipedia.org/wiki/Partial_fraction_decomposition, http://www.purplemath.com/modules/partfrac.htm, http://www.mathsisfun.com/algebra/partial-fractions.html
The reason why this is brought up is because
with the power of partial fractions, we can compute the inverse Laplace
transform of most rational functions. I’ll include one example just to show you
how it’s done!
That’s it for section 5.3! As long as you
remember partial fractions, you really should be golden.
Section
5.4 is entitled “Using the Laplace Transform to Solve Differential Equations.”
In other words, the previous sections were
more preface than anything else. They were merely the building the blocks for
you to get to this section. Hooray! With your newfound power of partial
fractions, Laplace transforms, inverse Laplace transforms, and propositions,
you’ll be able to solve differential equations (with initial conditions, too)!
You can also solve higher order differential
equations as well (say, order 4), and those equations are handled pretty much
the same way. Anyway, here’s an overview of the method:
We’ll be looking at the following initial
value problem:
We apply Laplace transform to this, where Y(s)
= ℒ(y)(s):
If y is a solution to the initial value
problem to our original differential equation, then ℒ(ay” +
by’ + cy) = ℒ(f) = F. We can substitute this into the
equation above and solve for Y. This means that
Something interesting to note about that final
equation is that the denominator is the characteristic polynomial of our
original differential equation.
Finally, two definitions:
Suppose ys is the solution of
Also, suppose yi is the solution of
Notice that although ys has initial
conditions equal to zero, it has the same forcing term (i.e. f(t)) as our
original differential equation. This is referred to as the state-free solution. On
the other hand, yi is the solution to a homogeneous equation, but it
has the same initial conditions. This is referred to as the input-free
solution. From our previous derivations, we have
It’s pretty plain to see that Y can be written
as Y = Ys + Yi, and from this we can see that y = ys
+ yi. Therefore, any initial value problems can be written as the
sum of its state-free and input-free solutions.
And that’s it for 5.4 and the evening! 5.5 is
going to be a bit more tedious than I previously thought, but it’s not that
long of a section. I have a test in this class coming up fairly soon, and thus
I would like to go about the test week the same way I did last time. I’d like
to not have to summarize new material whilst trying to remember the old
material.
Finally, a for-your-information type of thing,
there are 3 more sections to cover in chapter 5, and then I’m going to ask
about chapter 10 (in which we might look at the first two sections). If my
teacher says I should summarize those as well, that means we have 5 more
sections together before I’m off to bigger and better things (i.e. going onto
Tumblr and spending these hours there).
Perhaps I will write an epilogue to this epic
journey, just as a closer. We’ll cross that bridge when we come to it, though.
I’ll see you when I see you.




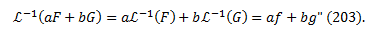






No comments:
Post a Comment