Section 5.5 is entitled “Discontinuous Forcing Terms.”
We’ve already looked at sinusoidal forcing terms. It’s high
time we look at piecewise continuous forcing terms.
Specifically, we’ll be looking at two kinds of functions:
the interval function and the Heaviside function.
Some properties about the Heaviside
function:
Also, the interval function Hab(t)
can be described using the Heaviside function:
You can also describe piecewise functions
in terms of the Heaviside function; for example, if we consider
We have the intervals 0 ≤
t < 4, 4 ≤ t < 6, and 6 ≤ t, so
we’ll use the interval functions H04, H46, and H6:
Now, for the Laplace transform of the
Heaviside function:
In particular, we have ℒ(H)(s)
= 1/s. Also, for the interval function Hab = Ha – Hb:
A proposition for you: “Suppose f(t) is
piecewise continuous and is of exponential order. Let F(s) be the Laplace
transform of f. Then, for c ≥ 0, the Laplace transform of H(t – c)f(t – c) is
given by
Back to our original example: We had translated
that piecewise function to 3H(t) – 8H(t – 4) + 5H(t – 6) + e7-tH(t –
6) and now we want to find the Laplace transform. The first three terms can be
handled with that handy proposition, and the last one can be rewritten as H(t –
6)e-(t-6)×e, and we can use that table from one of the previous
sections (http://differentialequationsjourney.blogspot.com/2013/11/52-54-where-you-refine-your-powers-of.html)
and this proposition to take care of it. Thus we have
Another proposition for you: “Suppose that
f(t) is piecewise continuous and is of exponential type. Suppose that F(s) = ℒ(f)(s).
Then
Finally, let’s talk about periodic functions.
A periodic function is one that has a repetitive pattern (as you can imagine).
The formal definition says that “f is periodic with period T (or
T-periodic) if f(t + T) = f(t) for all t” (222). Sinusoidal functions are
periodic, just for an example. Another example of a periodic function is called
a square wave. From a geometric perspective, if the function f is a T-periodic
function, then it repeats every interval of T. For this type of function, we
can define the window of f as
Finally (finally), here’s a proposition for
you: “Suppose f is periodic with period T and piecewise continuous. Let FT(s)
be the Laplace transform of its window fT. Then
That’s it for 5.5! I was planning on combining
5.5, 5.6, and 5.7 but I just don’t have the time to get them all written up. I’m
not on a time crunch or anything (quite the opposite, actually), but I really
do want to get them all up by Sunday. If I did that, I would only have those
two sections of chapter 10 (if that) and I wouldn’t be thinking of them after
my test.
Speaking of which, there shall be no summaries
up next week. This is because of my differential equations test.
I’ll see you in 5.6.




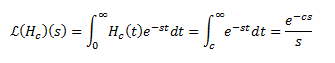




No comments:
Post a Comment