Section 4.4 is entitled “Harmonic Motion.”
I don’t think you can possibly understand how exciting this
is. We recently talked about this stuff
in my electronics class. At least, we talked about damping (which this is a
very watered down version of it). Hooray physics! :D
The motion for a vibrating spring has the following
equation:
In other physics news, in our bonus
section from Chapter 3 (the one about electrical circuits), we had the
following equation for RLC circuits:
When you compare these two equations,
they’re very similar. If we compare coefficients, the inductance L acts as the mass,
the resistance R acts as the damping constant, and 1/C (where C is the
capacitance) acts as the spring constant. Also, the derivative of the source
voltage (NOT energy, which is what I originally interpreted it as) acts as the external
force F(t).
Let’s divide our two equations by their
leading coefficients (L or m). Then they become
If we change some variables, i.e.
That final equation is known as the
equation for harmonic motion. Examples of this equation would be the vibrating
spring and RLC circuit. Hooray!
The constant c is called the damping constant,
and f is called the forcing term. Finally, this section consists of unforced
harmonic motion, meaning that f(t) = 0. This would make our harmonic motion
equation homogeneous.
The equation for simple harmonic motion
is when there is no damping (i.e. c = 0). The equation then simplifies to be
In the previous section, we know that for
characteristic equations with two complex conjugate roots, the general solution
will be
In this context, ω0
is called the natural frequency of
the spring. Also, the period of the solution x(t) is denoted as T, where T is
defined as 2π/ω0.
Now, let’s talk a bit about polar
coordinates.
Suppose we have a vector (a, b) in the
plane. When you write this is polar coordinates and when you assume (a, b) ≠
(0, 0), then there will be a positive number A (which is the length of the vector) and an angle φ
in the interval (-π, π] called the polar angle, in which
When you substitute these equations into our
general solution, we see we can write the general solution as
In this context, A is the amplitude of the
oscillation, and φ is the phase of the oscillation.
Your next question might concern how we find A
and φ.
Since we originally defined φ to be any angle
between –π and π, then we can’t just take the arctan of b/a, considering that
arctan only takes values between –π/2 to π/2. More importantly, this range
corresponds to points (a, b) where a > 0. So how do we compute φ when a <
0?
Now let’s consider the case when our harmonic
motion is damped (i.e. when c > 0). We’ll have the following differential
equation, characteristic equation, and roots:
Now we have a discriminant to worry about,
which means we have three cases to consider:
1. c < ω0; this called the underdamped case. The roots are
distinct and complex. The solution would be
2. c > ω0; this is called the overdamped case. The roots are distinct
and real. Also, λ1 and λ2 are both positive. The general
solution is
3. c = ω0; this is called the critically damped case. In this case,
the root is a double root, i.e. λ = -c. Our general solution is
Here are some websites for you: http://en.wikipedia.org/wiki/Simple_harmonic_motion
and http://scipp.ucsc.edu/~haber/ph5B/sho09.pdf
and http://wiki.ubc.ca/Simple_and_Damped_Harmonic_Motion
and http://hyperphysics.phy-astr.gsu.edu/hbase/oscda.html.
That’s it for 4.4! I’ve been busy and lazy,
and that combination leads to me not getting ahead with this blog. We just
started chapter 9 in my class, so it’s not like we’re catching up in any way
(knock on wood!). Hopefully I can get a lot of chapter 4 up this weekend. If
not, maybe I can get one more section up.
I’ll see you in 4.5!





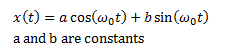





No comments:
Post a Comment