Section 2.4 is entitled “Linear Equations.”
A first order linear equation form:
If f(t) = 0, then this form is called
homogeneous. Otherwise, it is called inhomogeneous. The functions f(t) and a(t)
are the coefficients of the equation. Sometimes we can consider this equation
in an even more general form:
This is still linear because you can just
divide the b(t) over to put x prime by itself.
Something really important to note about linear
equations is that x and x prime appear alone and only to the first order. Note:
“…we do not allow x2, (x’)3, xx’, ex,
cos(x’) or anything for complicated than just x and x’ to
appear in the equation” (47).
 |
| Stay away, tricky calculus. |
Kind of as a summary, here’s a small list
of what’s considered linear and what’s not:
Linear equations can be solved exactly.
Let us start with a general equation and show this:
So, when solving homogeneous equations
for a general solution, there’s a basic process you can follow:
1. Separate variables
2. Integrate, rewrite constants as other
constants if necessary, etc.
3. Go celebrate because you’re done
There are a couple more steps when
solving an inhomogeneous equation.
So here are the steps:
0. For these steps, I’m referencing the
following equation:
1. Rewrite as
2. Multiply by an integrating factor:
3. Integrate:
4. Solve for x(t).
Here’s an example (because the whole
integrating factor thing should make more sense once you’ve seen an example):
Multiply by the integrating factor:
There’s also an alternate solution method
for solving these equations, and I’m going to use a pretty generic example to
show how it’s done.
The function v that we used to substitute
is unknown (obviously). It is sometimes called a variable parameter, and
therefore the method is called variation of parameters.
Now, the steps:
0. For these steps, I’m referencing the
following equation:
1. The associated homogeneous equation is
And the particular solution to this
equation is
2. Substitute
the variable parameter v times the particular solution of y in for y to find v.
You can also just remember this tidbit about v:
3. Write down a general solution:
 |
| Just in case you weren't aware. |
That’s all for this section. Note now
that in my class, we skip over section 2.5, so the next post will be section
2.6.
Sorry there wasn’t much attempt of
funniness. Now you know I’m not actually that funny.
 |
| I'll try harder next time. (narsbusiness.com) |







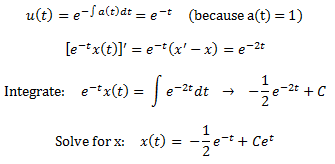





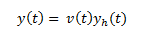

No comments:
Post a Comment