Section 7.2 is entitled “Systems of Linear Equations with
Two or Three Variables.”
Let’s consider the equation 5x + 7y = 9. There will be a lot
of different vectors that will satisfy this equation (i.e. solve it). The set
of all of these vectors will be known as the solution set. In this case, the
solution set would be a line in the xy-plane.
If we solve for y, we’ll get y = (9 – 5x)/7. This can be
rewritten as
This equation is known as the parametric
representation of the line modeled by our original equation. In this case, x is
a free parameter, because any value of x will be a point on the line. For
example, when x = 1, a point (1, 4/7)T would be on the line.
Generally, we would start at x = 0, and then that point would be called p. Then, for any value of x, we would
add multiples of the vector v = (1,
-5/7)T.
(Reminder: The T is a transpose, and it’s
just being used as a handy way to write vectors horizontally, despite their
vertical traits.)
Time for our favorite words again!
Ax
= b is said to be homogeneous if b is equal to the zero vector, which the
book denotes by 0. If b is not equal to the zero vector, then
the system is inhomogeneous.
And now for a definition:
“A line is Rn is a set of the form
where p and v ≠ 0 are vectors in Rn. [This equation above] is called a parametric
equation for the line” (284).
The vector p is the point corresponding to t = 0. Our vector v gives us the direction of the line.
Now let’s look at two linear equations with
two unknowns. Let’s consider the following equations:
5x + 7y
= 9
x – y =
0
Separately, the solution sets for these
equations are lines. Since we want the solution for both equations at the same
time, then we’re looking for the line in which these equations intersect.
Either there will be one point they intersect, or they will never intersect
(because then they would be parallel).
We could solve this equation using algebra, by
substituting x = y into our first equation and then getting answers. We would
get 12y = 9, which would lead us to the new system of equations x – y = 0 and
12y = 9. We could add 12 times the first equation to the second and solve for
x. This operation is called elimination (because our goal is to eliminate
variables). Or you could just solve for y in our second equation and plug into
the first equation to solve for x. Either way, you get the answer to be x = y =
9/12 = 3/4.
If we solved the second (i.e. last) equation
first in our new system of equations and then solve the first equation, then we
would be performing the method of back-solving. However, we usually have too
difficult of equations and unknowns to simply back-solve and be on our merry
way. We will usually use elimination to solve our equations.
Let’s rewrite our system in matrix notation:
If we define A as our coefficient matrix and b as the right hand side, we can
rewrite this system as A(x y)T = b. All of our information can be easily compacted into one larger
matrix, called the augmented matrix.
We could also solve this matrix to look like
our second set of equations, i.e. adding -5 times the first row to the second
row. Then we would get
If the equations in a system are parallel,
then they will have no solution. We call these systems inconsistent. We could
also be presented with a system with equations that are multiples of each
other. In this case, their solution sets would be the exact same. In conclusion
of this, there are three and only three outcomes for solving a system of
equations:
1. One point
2. A line
3. No solutions
Our first case happens often. The other two
cases are called degenerate cases.
A bit more on homogeneous systems: They will
always be consistent. So if you are presented with a homogeneous system, then
you will never get “no solution” as the answer. The solution will either be the
origin, or the line going through the origin.
If we were offered the line x + 2y – 4z = 5,
then that equation is in three dimensions. We could solve this equation for x
and get x = 5 – 2y + 4z. Then we would have the solution set be
Similar to the equation in two dimensions,
this would be the parametric representation for a plane. In this
representation, we have two free parameters: y and z. We would start at our
point p = (5 0 0)T and
adding a linear combination of what is called v1 and v2.
The formal definition:
“A plane in Rn is a set of the form
where p,
v1, and v2 are vectors in Rn such that v1 and v2 are not multiples of each other. [The equation above]
is called a parametric equation for the plane” (287).
If we were to look at two equations with three
unknowns (which will make planes), then we know by geometry the solutions will
have three possibilities:
1. The planes intersect in a line
2. The planes are the same plane and thus the
solution set will be a plane
3. The planes are parallel and there will be
no solution
In order to solve these equations, we shall
use matrix notation and elimination. In some cases, we can eliminate some
things and then make it possible to back solve. Then, in that case, we may be
able to assign any value to a certain variable, say z, and then we can easily
solve for numerical values for the other two variables, say x and y. In this
case, we would call z a free variable and then we can set z = t (it’s the book
way of saying, “hey, this can be any number”). This means the solution sets for
planes will take on the following form:
This is just an example, but shows what our solution sets would look like.
For three equations and three unknowns, we
will use matrix notation and elimination to prepare for back-solving. It sounds
fairly simple, but it really can get messy. If you pick the right numbers, the
answer can look gross. The solution sets for three equations with three
unknowns will either be
1. One point
2. A line
3. A plane
4. No solution
If the equation is homogeneous, then the
origin will always be a solution, which means homogeneous solutions will always
have a solution. This means our possibilities for homogeneous systems are
1. The origin
2. A line though the origin
3. A
plane through the origin
Notice that we can have a single point as a
solution for one, two, or three dimensions. This will look similar in any
dimension. We also have lines in two dimension and lines and planes in three
dimensions. They have common features that the book describes well:
“First, if we can move in a particular
direction…we can move arbitrarily far in that direction. We can summarize this
by saying that the set in infinitely long. Second, if there
are two are two directions in which we can move, as in a plane, then we can
move in any linear combination of those directions. We can summarize by saying
that the solution set is flat. Finally, a line in the plane,
or a line or plane in 3-space, does not take up much room. Both have negligible
extent in most directions. We can summarize that by saying that the solution
set is thin” (290).
When we go into higher dimensions, we can’t
really visualize it anymore and our intuition is lost. But we might think that
these characteristic (long, flat, and thin) might also be used to describe
solution sets in higher dimensions.
I guess we’ll find out when we go to section
7.3, but for now this is where we will end.
I’ll see you when I see you!





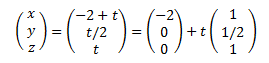
No comments:
Post a Comment