Section 6.2 is entitled “Runge-Kutta Methods.”
This is just another numerical solver for differential
equations. This is similar to Euler’s method because this method is also a
fixed-step solver. Our step size is still the same as last time: h = (b – a)/N.
Like last time, we’ll set t0 to be a, and t1 would be t0
+ h (= a + h), etc., until the final value tN = a + Nh = b. Like
Euler’s method, our dependent variable (in this case, y) will be chosen
iteratively.
At this point you might be asking, “So what’s the difference
between this method and Euler’s?”
To which I answer, “Hold your horses, buckaroo. We’re
getting to the best and worst part about this method right now.”
The difference is that it’s more difficult to find a
geometric interpretation of this method, as compared to Euler’s. Hooray!
(Let me just point out that the section on Euler’s method is
twice as long as our current section. This makes me fear for my life as I move
onto the next page.)
So there are different orders to the Runge-Kutta method. The second-order version of this
method is also called the improved Euler’s method. We start with our initial
point (t0, y0) and we compute two different slopes from
it:
If we think back to what we did in Euler’s
formula, we see we replaced the slope f(t0, y0) with the
average of our slopes. This isn’t intuitive or anything on the surface, but
Taylor’s formula tells us that the truncation error improves drastically with
this replacement. So let’s define all of our values inductively:
So when we compute maximum error from
this, we get
Our constant L is the same as last time,
but M is not. Note: “…again it depends only on f(t, y). Its exact formula is
not too useful” (256).
The power of our step size h (in both
Euler’s method and this method) is called the order of the solver. This is
where we get the second-order part of the second-order Runge-Kutta method
(because the h is squared…). This would make Euler’s method a first-order
method.
Our good and bad news about the error is
basically the same as Euler’s method. The good news comes from our step size,
but it’s even better news now, because we can pick incredibly small steps and
BOOM our error can get really low. However, we still have the problem with the
interval b – a. This means this method becomes incredibly unreliable over long
intervals.
The final topic we shall be covering in
this section is the solution method.
It’s widely used and fairly fast. It’s also much more accurate than Euler’s
method. It’s known as the fourth-order Runge-Kutta method.
So we have three cases now: Euler’s
method, the second-order and the fourth-order Runge-Kutta method. For all three
of these methods, we see that yi is found by adding yi-1
to some sort of average of the slopes. In Euler’s method, the average is just
one slope, while the average of the slopes from the Runge-Kutta methods is
slightly more difficult.
The constant L is the same as before,
while M is different from both of our previous methods. Again, it doesn’t
matter enough to be listed. We see now why this method is called a
fourth-order, since the step size is to the fourth power. Something highly
important to note about this method is that it produces the most accurate of
results in terms of error.
Okay, that’s it for section 6.2 (I know,
it was a pretty fast one this time). The next section shall be in chapter 7, so
I’ll meet you there.

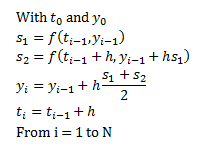



No comments:
Post a Comment