Section 2.6 is entitled “Exact Differential Equations.”
Let’s look at a very general differential equation
You work this differential equation like
you would work any other differential equation; you can solve for y(x)
and our differential equation will satisfy it. Recall that back in our
discussion with separable differential equations, we talked about solutions
that are defined implicitly. This means they take the form
In this equation, x and y are treated the
same. There is no distinction between the two. We can do this for any
differential equation. This leads us to a definition:
A differential form for x and y has an
expression like
P and Q are still functions of x and y,
like our first equation. The dx and dy in the expression are called
differentials. Y is still the dependent variable, so it can still be written as
y(x). This means
Y is a solution to our original
differential equation if and only if
This is just another way of writing our
original differential equation.
Now, let’s suppose that the solutions for
our differential equation (we can refer to either form for this) are given
implicitly by F(x, y) = C. The level sets defined by our solutions are called
integral curves.
 |
| (Wikipedia) |
The picture shows integral curves for
differential equation
Also, here’s a website that draws
solution curves for pretty much any equation you want: http://faculty.fortlewis.edu/Pearson_P/jsxgraph/slopefield.html
Moving on, we said F(x, y) = C gives a
general solution for the following equation:
So y = y(x) is defined by our general
solution. When we take partial derivatives in terms of x, we get
If you don’t remember what a partial
derivative is or how to take a partial derivative, I’ll leave this handy
website for you here: http://tutorial.math.lamar.edu/Classes/CalcIII/PartialDerivatives.aspx
We already said y(x) is a solution to our
differential equation, so we graciously receive
When we compare our two previous
equations, we see that
If we define the latter part of our
previous equation as μ(x, y), then our
equation simplifies to be
Therefore, in order to find a solution to
our original differential equation, we must find the functions μ
and F that satisfy our previous equations.
Right now, we’re going to look at when μ
= 1, which would make our equation:
Note: “The differential of a continuously
differentiable function F is the differential form
A differential form
is said to be exact
if it is the differential of a continuously differentiable function” (65).
In other words, the form “P dx + Q dy” is
exact if and only if there’s a function F(x, y) such that
This means dx = dy, or
Also, if the form “ω
= P dx + Q dy” is exact and equal to dF, then the general solution to “dF = P
dx + Q dy = 0” is given by F(x, y) = C.
Here’s an example (and there are two
others on Khan Academy so you could watch all of them if you’d like): https://www.khanacademy.org/math/differential-equations/first-order-differential-equations/exact-equations/v/exact-equations-example-1
It’s fairly easy to solve a differential
equation when its variables are separated. In terms of our original
differential equation, that form would be P(x)dx + Q(y)dy = 0. The solution to
this would be F(x, y) = C, where
From this, two questions can arise:
1. When ω
= P dx + Q dy, how do we know if it’s exact?
2. If it is indeed exact, how do we find F
such that dF = P dx + Q dy?
To answer these questions, let us use the
equation from our first question, where P and Q are continuously
differentiable. Here’s a two part theorem about this equation:
(a) If ω
is exact, then
(b) If this equation is true in a rectangle
R, then ω exact in that rectangle.
The proof is done by hand for you (you’re
welcome, although it wasn’t that hard):
So to solve an exact differential
equation, we have two methods to do so:
1. Find F by guess-and-check (but the book
is for grownups and the grownup version of this is “inspection and
experimentation”)
2. Use the second part of our proof. Reminder: If “P(x, y) dx + Q(x, y) dy =
0” is exact, the solution is F(x, y) = C, where F is found by solving
Here are some steps to follow:
You could solve in terms of Q (it would
be with respect to y instead of x) first, but there would be a different
“constant” of integration (instead of phi).
Moving on:
Let’s flashback to where we said in order
to solve “P dx + Q dy = 0” we need to find a μ
and F that satisfy
Here’s a new definition: “An integrating
factor for the differential equation “ω=P
dx + Q dy = 0” is a function μ(x, y) such that the
form “μ
ω = μ(x, y) P(x, y) dx + μ(x, y) Q(x, y) dy” is exact” (69).
In order to find a general solution to P dx +
Q dy = 0,
1. Find an integrating factor μ so that “μ
P dx + μ Q dy” is exact
2. Find a function F such that “dF = μ
F dx + μ Q dy”
Our general solution takes the form F(x,
y) = C.
So in this context, let’s redefine
separable and linear equations.
An equation is separable if there is an
integrating factor that separates the variables in the form P(x) dx + Q(y) dy =
0. This means the solution is given by
Back in section 2.2, there was a special
case in the form
So the integrating factor would be q(y),
and the equation transforms to “p(x) dx – q(y) dy = 0”
Linear equations have a special form
Back in section 2.4, we solved a linear
equation using an integrating factor μ(x)
If μ(x) satisfies this
equation, then “μ(x)[a(x) y + f(x)]dx - μ(x)dy = 0” is exact. This means the
general solution is
Moving on, suppose ω = P dx + Q dy and we want
a μ such that “μ ω = μ P dx + μ Q dy” is exact. This means μ must satisfy
However, there really is no procedure for
solving this equation. It would make it easier to have an integrating factor
that only depends on one variable, because then this equation would be so much
easier to solve. Let’s just do that for now.
So let’s find out when P(x, y)dx + Q(x, y)dy =
0 has a μ(x) that only depends on x. This means μ does not depend on y (common
sense) so our equation would simplify to be
So μ will only depend on x solely if the
following equation solely depends on x:
If this is true, then μ(x) is a solution to
More generally, “P dx + Q dy” will have an
integrating factor that only depends on one variable under these conditions:
Moving on, here’s a handy definition of a
homogeneous equation: A function G(x, y) is homogeneous of degree n if G(tx,
ty) = tn G(x, y) for all t > 0 and x ≠ 0, y ≠ 0
Here are some examples of homogeneous functions:
Their homogeneous degrees are -2, 0, 3, and 1,
respectively.
Here are some examples of non-homogeneous
functions:
“P dx + Q dy = 0” is homogeneous if P and Q
are homogeneous to the same degree. We could also put these equations into a
solvable form using the substitution y = xv (where v is a new variable). Here
are some steps to make this easier:
1. Make the substitution y = xv
2. Look for an integrating factor to separate the
variables.
Let’s start with P(x, y)dx + Q(x, y)dy = 0,
where P and Q are both homogeneous to the same degree.
If y = xv, then P(x, xv)dx + Q(x, xv)(v dx + x
dv) = 0
We stated above that P and Q are homogeneous. This
means
P(x, xv) = xn P(1, v) and Q(x, xv)
= xn Q(1, v)
When we use this, our differential equation becomes
[P(1, v) + v Q(1, v)]dx + x Q(1, v) dv = 0
Our integrating factor would be
This will separate our variables, so it leaves
us with
Then we can substitute v = y/x back into our
function so we can have our y’s back in the equation.
Finally, here are some examples from the book
that may or may not help you understand this better.

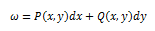
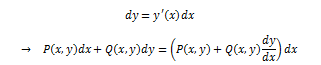

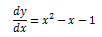




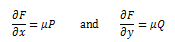
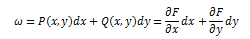






















No comments:
Post a Comment