Section 2.2 is entitled “Solutions to Separable Equations.”
Let’s start with the definition of a separable equation.
Surprise, surprise! This type of equation can be rewritten with its independent
and dependent variables separated from one another.
The book uses the following equation as their example (so I’m
going to use this example as well):
N is a function and lambda is a constant. This equation is use
in problems involving the half-life of radioactive elements. In this example, N
is the dependent variable and t (which stands for time) is the independent
variable.
Now, I shall demonstrate the art of separating equations.
Now we can go one of two
ways: the physics way or the tricky calculus way.
My teacher provided the
following diagram to explain why we should go the physics way:
 |
| Note: not his diagram, rather my crappy Paint version of his diagram |
This is what I saw:
(Note: Just kidding. But
really physics is easier to understand, never mind legitimacy)
In all reality, the tricky calculus way isn’t
that bad. It’s just easier to do the physics way because that’s just how
physics rolls.
Now, we separate the “N” variables
from the “t” variables. Note that there are no t variables on site (besides the
dt) but lambda is included in the “t” variables because it’s a constant.
And we integrate!
This type of equation is
also known as an exponential function, because the solution contains an
exponent.
This is the basic method for
solving separable equations:
1. Separate variables
2. Integrate
3. Solve for the dependent
variable.
Note that separable
equations will either take the form of
Adding (or subtracting) is
not separable. Tricky calculus cannot help us save the day :(
Here’s a definition from the
book (throwback to last section):
General solution: “A family
of solutions depending on sufficiently many parameters to give all but finitely
many solutions” (30).
In other words, a general
solution might not give a solution to every initial value problem thrown its
way (for example, when division by zero is a factor).
Here’s another definition
(and another example of a separable equation):
Newton’s Law of Cooling: “The
rate of change of an object’s temperature is proportional to the difference
between the temperature and the ambient temperature” (31).
By the way, the example
given to show Newton’s Law of Cooling involves a can of beer. Is this is a
college textbook or what?
The unsolved separable
equation for Newton's Law of Cooling is as follows:
A is the ambient temperature
(for instance, room temperature or outside temperature). T0 is the
initial temperature of the object. The constant k can be solved for and then you’re
all good to go with solving for lots of things!
Here’s a link to someone who
actually took the time to solve the Newton’s Law of Cooling equation with steps
and stuff: http://www.math.wpi.edu/Course_Materials/MA1022A96/lab2/node5.html
Something to note about separable
equations is that sometimes solving after integration is very difficult, and
sometimes not even the trickiest of calculus can simplify our solution to just
one dependent variable.
For example, y = 5x + 2 is
simplified.
For non-example, the
following equation cannot be simplified:
Some definitions for you:
Explicit: formula as a
function in terms of the independent variable (our example shows this).
Implicit: the opposite of
explicit. Our non-example shows this.
Finally, I shall show you
why the separation of variables step (i.e. the physics way of solving separable
equations) works.
Nevertheless, say we start
with the following equation:
Note this is very similar to
the h(y)dy = g(t)dt step we do in the physics version.
Mathematics deems this
step to be meaningless (since dy and dt by themselves don’t make much sense
without integrals). I understand and appreciate the validation of the physics
way, and I hope you do as well.



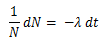


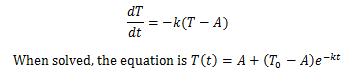

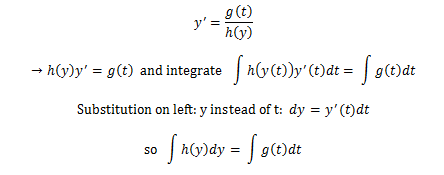
No comments:
Post a Comment