As a side note, I use quotes taken directly from the book sometimes.
You may not think that is the consistency of a summary, but I think the best
summaries involve the words of people who really know what they’re talking
about. These three gentlemen who wrote my math book have far more experience
and wisdom about differential equations than I do. Therefore I think I am just
in my actions in using quotes direct from the text.
Before I begin with summaries and such, I thought I’d share
with you my thoughts about the most serious paragraph in the preface, entitled
“Mathematical Rigor.”
First of all, I knew this was going to be super serious when
I read the sentence “Mathematical ideas are not dodged.” Don’t ignore the ideas
behind math, people! They’re super important. Also, the word “dodged” seems
like a British word to me (someone else has to feel this way as well!). This
makes me think that one or more of the authors must be British. I looked up the
authors of my textbook and I now know that Polking and Boggess are not British
but I can’t find any birth information on Mr. Arnold. He works in California so
I can’t just assume he’s British. My hypothesis has failed and I now turn to
the “they’re very smart gentlemen” hypothesis.
Anyway, this paragraph really sprinkles in the emphasis
behind understanding the theorems and proofs working in the shadows of the
textbook. Note: “The authors believe that proof is fundamental to mathematics,
and that students at this level should be introduced gently to proof as an
integral part of their training in mathematics” (xii). I’m fine with the fact
that these authors are humble enough to refer themselves in the third person,
but I also think they’re pushing math pun with “integral” and that’s just
amazing.
Anyway, onto the sections.
Chapter 1 is entitled “Introduction to Differential
Equations.” Section 1.1 is entitled “Differential Equation Models.”
It’s an introduction to the book, so it’s just introducing
what the book is going to teach us, in a sense. The first four paragraphs
before the first section state there shall be quite a few examples from physics
and chemistry and other subjects that include and are related to differential
equations. There is also an emphasis of the importance of differential
equations and the level of usefulness in real life. Note: “If it were not true
that differential equations were so useful, we would not be studying them…”
(1).
In the first section, there are a lot of examples of how
differential equations are used in everyday life. The topics of study for
differential equations listed are mechanics, population models, pollution, and
personal finance, along with others (aptly titled “other examples”). My
personal favorite is mechanics, because Isaac Newton is involved and so is
physics. He was key in the development of differential equations because he
just so happened to invent calculus and a lot of classical physics. There could
be hundreds of examples for differential equations (including but not limited
to electricity and magnetism) but the major point is that this kind of modeling
the world due to its reliability and precision.
Section 1.2 is entitled “The Derivative.”
The section starts off with the question, “What is a
derivative?” Five answers are given: the rate of change of a function, the
slope of the tangent line to the graph of a function, the best linear
approximation of a function, the limit of the quotients, to which the following
function was given:
and the final answer to the question
“What is a derivative?” was given in a table of derivatives, which included the
simple ones such as the constant and the cosine of x.
When the derivative is referred to as the
rate of change, it is also known as the modeling definition of the derivative.
When the derivative is referred to as the slope of the tangent line, it is also
known as the geometric definition of the derivative. When the derivative is
referred to as the best linear approximation, it is also known as the algebraic
definition of the derivative. When the derivative is referred to as the limit
of difference quotients, it is also known as the limit quotient definition.
And, of course, the formulaic definition is the list of formulas.
 |
| Crappy Paint version of the slope of the tangent line (geometric definition) |
Section 1.3 is entitled “Integration.”
Just like the last one, this section starts off with a
question. This time, the question is “What is an integral?” The following three
answers are given: the area under the graph of a function, the anti-derivative,
and a table of integrals.
The area under the graph is also known as the definite
integral. It is the most fundamental definition of the integral.
The anti-derivative is synonymous with the indefinite
integral. There’s a handy little equivalence in the book that states that if f
is continuous,
Also, the fundamental theorem of calculus
is back! It’s what connect
s the definite and the indefinite integral. Of
course, it is stated that if f prime = g, then
The authors state that although the table
of formulas is a handy skill to have, it does not lead to a deep understanding
of integration. However, the authors go on to state all the approaches (the
area, the anti-derivative, and the formulas) are important. But the authors
also stress the importance of finding anti-derivatives, and so do I. When we
move onto solving differential equations (i.e. in the next chapter of the book)
finding anti-derivatives is a crucial part for solving them.
When solved with a constant (in other
words with an indefinite integral) it is called a general solution. When there
is an initial condition (for example, when solving the equation y prime = t*e^t and it satisfies y(0) = 2) it is called an
initial value problem.
Chapter 2 is entitled “First-Order
Equations.” Section 2.1 is entitled “Differential Equations and Solutions.”
The chapter includes a lot of definitions
so I’m just going to get those definitions out of the way.
Ordinary differential equation: “equation
involving an unknown function of a single variable together with one or more of
its derivatives” (16).
Order: in a differential equation, it is “the
order of the highest derivative that occurs in the equation” (17).
On this note, a first order equation
would only have the first derivative, while a second order equation would have
second derivatives.
Normal form of a first-order differential
equation takes the form y prime = f( t, y).
The answer to a differential equation
that contains constants is called a general solution. When there are initial
conditions and the equation is solved completely, the solution is called a particular
solution. A differential equation with an initial condition is called an
initial value problem.
Interval of existence: “the largest
interval over which the solution can be defined and remain a solution” (19). This
comes in handy when there are solutions that have undefined areas (say, when
the denominator of a function can be equal to zero or when a natural log function
can have a negative number inside of it).
After this, there is a section on using
other variables besides y and t (which are the go-to variables for differential
equations). I don’t know why this section is included (unless a lot of students
got very confused over why the functions suddenly contained some s’s and g’s)
but I thought I would mention it, nonetheless.
Also included in the section are things called
direction fields. They show the slopes at specific points of solved
differential equations. It’s worth mentioning because there are a couple of
pages about direction fields. A curve can be draw using the direction fields,
and that curve is called a solution curve. On that note, a solution curve is
the graph of a general solution (or many general solutions) for a first-order
differential equation. Finding an approximate solution curve using the
direction field is called Euler’s method, which is defined as “an algorithm
used to find numerical solutions of initial value problems” (22).
Sometimes, the direction fields have
horizontal slopes. These points are called equilibrium points and the solutions
are called equilibrium solutions. There can also be multiple solution curves
taken from a direction field.
That’s all for now, I’m afraid. I’ll be
writing the next one up soon.

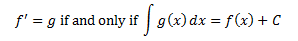

No comments:
Post a Comment