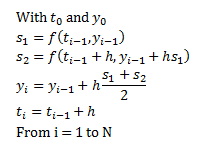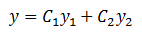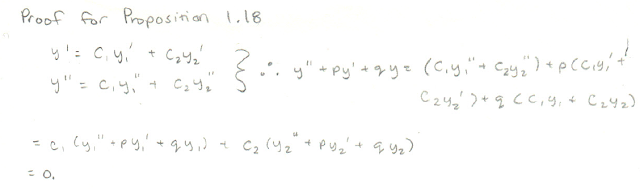6.2, i.e. the other (more improved) (better) numerical solver.

Section 6.2 is entitled “Runge-Kutta Methods.”

This is just another numerical solver for differential equations. This is similar to Euler’s method because this method is also a fixed-step solver. Our step size is still the same as last time: h = (b – a)/N. Like last time, we’ll set t₀ to be a, and t₁ would be t₀ + h (= a + h), etc., until the final value t_N = a + Nh = b. Like Euler’s method, our dependent variable (in this case, y) will be chosen iteratively.

At this point you might be asking, “So what’s the difference between this method and Euler’s?”

To which I answer, “Hold your horses, buckaroo. We’re getting to the best and worst part about this method right now.”

The difference is that it’s more difficult to find a geometric interpretation of this method, as compared to Euler’s. Hooray!

(Let me just point out that the section on Euler’s method is twice as long as our current section. This makes me fear for my life as I move onto the next page.)

So there are different orders to the Runge-Kutta  method. The second-order version of this method is also called the improved Euler’s method. We start with our initial point (t₀, y₀) and we compute two different slopes from it:

If we think back to what we did in Euler’s formula, we see we replaced the slope f(t₀, y₀) with the average of our slopes. This isn’t intuitive or anything on the surface, but Taylor’s formula tells us that the truncation error improves drastically with this replacement. So let’s define all of our values inductively:

So when we compute maximum error from this, we get

Our constant L is the same as last time, but M is not. Note: “…again it depends only on f(t, y). Its exact formula is not too useful” (256).

The power of our step size h (in both Euler’s method and this method) is called the order of the solver. This is where we get the second-order part of the second-order Runge-Kutta method (because the h is squared…). This would make Euler’s method a first-order method.

Our good and bad news about the error is basically the same as Euler’s method. The good news comes from our step size, but it’s even better news now, because we can pick incredibly small steps and BOOM our error can get really low. However, we still have the problem with the interval b – a. This means this method becomes incredibly unreliable over long intervals.

The final topic we shall be covering in this section is the solution method. It’s widely used and fairly fast. It’s also much more accurate than Euler’s method. It’s known as the fourth-order Runge-Kutta method.

So we have three cases now: Euler’s method, the second-order and the fourth-order Runge-Kutta method. For all three of these methods, we see that y_i is found by adding y_i-1 to some sort of average of the slopes. In Euler’s method, the average is just one slope, while the average of the slopes from the Runge-Kutta methods is slightly more difficult.

However, the payoff is a much improved error.

The constant L is the same as before, while M is different from both of our previous methods. Again, it doesn’t matter enough to be listed. We see now why this method is called a fourth-order, since the step size is to the fourth power. Something highly important to note about this method is that it produces the most accurate of results in terms of error.

Okay, that’s it for section 6.2 (I know, it was a pretty fast one this time). The next section shall be in chapter 7, so I’ll meet you there.

6.1: What we're really going to be talking about.

Just kidding, everyone! I was going off the incorrect list, assuming we were going through the book in order. Instead, I should have been looking at the schedule that says we will be going to chapter 6 now.

Think of section 4.1 as another bonus section. Hooray!

Anyway, onto the next summary…

Chapter 6 is entitled “Numerical Methods.”

Section 6.1 is entitled “Euler’s Method.”

Since the beginning of our differential equation journey, we have been using numerical solutions of our ordinary differential equations. However, a numerical solution is less of a solution and more of an approximation. This means we make an error while finding our solution, which now is the time to understand the error.

Let’s consider our already well-known initial value problem

Let’s also be interested in our solution on a certain interval, say a ≤ t ≤ b. Let’s also assume the solution exists on this interval. As always, we will denote this solution by y(t).

Here’s a definition for you: A numerical solution method (also known as a numerical solver) will choose a specific and discrete set of points (i.e. t₀, t₁, t₂, … , t_N) within our interval and values (i.e. y₀, y₁, y₂, … , y_N) such that each value y_i is approximately equal to y(t_i) (where i = 0, 1, 2, … , N). Our initial condition is our first point and will start this method off for us.

The first method we will look at is Euler’s method. This is an example of what is called a fixed-step solver, which means we chose the set of values of the independent variable so that for our interval, we get N equal subdivisions or subintervals. In order to do this, we shall set a step size h, which is equal to (b – a)/N.

The idea is that we’re using the tangent line to approximate the solution. We start out with the tangent line of our initial condition, and we make our first step (t₁). Then, once we have computed t₁ and y₁, we use those values to make our second step, and so on. The general method is as follows:

Something to take note is that y­_i only depends on the previous calculations (t_i-1 and y_i-1). This solver is thus known as a single-step solver because of this property.

For this method, the magnitude of the error usually increases with each step. Sometimes this isn’t so, but for the most part, this is a thing that happens.

There are two sorts of error involved in Euler’s method. In the actual process, there is truncation error, and there is round-off error by the computer, calculator, or by hand.

Round-off error is pretty straightforward: you make a calculation, and you round off to, let’s say, three decimal places. You might be rounding up or down depending on your digits. So there’s a probability of an error being produced in the last place of your calculation. However, the process that calculators and computers use to make calculations has such a high accuracy that the round-off error is usually negligible. Sometimes, this isn’t the case. However, negligible round-off error is almost always a thing to look forward to when we have numerical solutions of ordinary differential equations. Therefore, we won’t be talking about round-off error anymore.

This leaves us with truncation error. In order to really understand truncation error, we would have to look at Taylor’s formula. In order to avoid spitting more formulas at you, here’s some handy websites for you to look at:

http://maecourses.ucsd.edu/~smicheli/mae107-s209/files/Taylor.pdf (page 3)

http://en.wikipedia.org/wiki/Truncation_error

The point of bringing up Taylor’s formula is to see the remainder in Taylor’s formula. This is a simple error that is made in each step. This error is truncation error.

This graph shows the first two steps of Euler’s method. The error in the first step is purely truncation error (as shown by the darker gray line between (t₁, y(t₁)) and (t₁, y₁)), while there are two sources of error for the second step. The error below the gray line is truncation error, while the error above the gray line is what is called propagated truncation error. This is the error propagated by the solution error. It’s a little hard to see from my picture, but sometimes the propagated truncation error can be much larger than the original truncation error. As you increase in the number of steps, the sum of the propagated truncation errors from the previous steps plus the truncation error of the current step itself adds up to the total error, and it’s a lot.

We can analyze the total error.

With this error, the constants M and L depend only on the function f(t, y).

In this case, R is a rectangle in which the solution curve is contained.

There is both a good thing and a bad thing for our error. This is a good thing because the step size h is a factor in the error. This means we can make our step size super small and the error will also be super small. The bad news is (b-a) is also a factor. This means for large intervals, the error gets super large. However, this is a thing for all numerical solvers.

Solution methods can be applied to systems of differential equations. You know what’s funny about this? My accidental bonus section (4.1) is where we get the example for this. Remember the spring and mass system?

Okay, that’s it for 6.1. I’m going to summarize 6.2 for next time (I promise, I’m looking at the correct schedule this time). I’ll see you when I see you. 

4.1: The exposition to conquer all exposition

Chapter 4 is entitled “Second-Order Equations.”

Section 4.1 is entitled “Definitions and Examples.” (With a section title like that, you know this summary is going to be filled with fun and happy times.)

This section is filled with lots of propositions and theorems and physics, so it won’t be so bad. Consider this the exposition to the next five sections you will see on this blog. Hooray! However, the thing about theorems is that there should be a proof alongside it, which means I have to write those up. Hooray.

A second order differential equation is similar to a first order differential equation, with the independent variable and the dependent variable and the first derivative, except (surprise, surprise) the second-order has a second derivative as well. Assuming we can solve for this second derivative, our equation would then have the form

The solution to this differential equation is what is called a twice continuously differentiable function y(t), where the form would be

An example of a second order equation would be Newton’s second law (F = ma), since acceleration is the second derivative of position. The force is usually a function of time, position, and velocity, so the differential equation would have the form

A special type of second order differential equations is linear equations, which have the form

As with the first order linear equations, the p and q and g are called coefficients. And, just like last time, y^’’ and y^’ and y must appear to first order. The right hand side of the equation (i.e. g(t)) is called the forcing term because it usually arises from an external force. If this forcing term is equal to zero, then the equation is considered homogenous. This means the homogeneous equation associated with our linear equation is of the form

Another example of a second order differential equation is the motion of a vibrating spring.

I drew a picture similar to the one in the book. The first position of the spring (marked with the (1) thingy on the right) is called spring equilibrium. This is where the spring will rest without any mass attached. The (2) position is called spring-mass equilibrium. This is the position x₀ where the spring is again in equilibrium with a mass attached. There are two forces acting on the spring: gravity and what is called the restoring force for the spring. We will denote the restoring force with R(x) since it depends on how far the spring has stretched. Equilibrium means the total force on the weight is zero, which means the equivalent force equation for this system is

In the (3) position, the spring is stretched even further and is no longer in equilibrium, which means the weight is probably moving. Allow me to remind you that velocity is the first derivative of position. (This will come in handy later.)

Now, for (2) we made a force equation for the system. Let’s do this for (3) as well. We still have gravity and the restoring force acting on the system, but now we also have what is called a damping force, which we will denote as D. The book defines this force as “the resistance to the motion of the weight due to the medium (air?) through which the weight is moving and perhaps to something internal in the spring” (138). The major dependence that this damping force has is velocity, so we can write this force as D(v). Finally, we’ll add in a function F(t) for any external forces acting on the system.

If we write acceleration as x^’’ (meaning the second derivative of the position), then we can write our total force on the weight, ma, as mx^’’. This means we can write our second order differential equation for the forces acting on this system as

Now, you might be asking “Well, how do we find restoring force?”

To which I say, “Physics!”

Hooke’s Law says that the restoring force is proportional to the displacement. This means the restoring force is

There’s a minus sign as to indicate the force is decreasing the displacement, which means k, which is known as the spring constant, is positive. Something to note about Hooke’s Law is that it is only valid for small displacements. So if we assume our restoring force follows Hooke’s Law, then our equation becomes

Just assuming that there is no external forces acting on the system, and that the weight is in spring mass equilibrium (position (2)). This means x is a constant, so its first and second derivatives are zero, which would make the damping force equal to zero. This means our equation would become

The book discusses units very quickly so I will too. The book uses the International System (as it should), where the unit of length is the meter (denoted m), the unit of time is the second (denoted s), and the unit of mass the kilogram (denoted kg). Everything other unit is derived from these fundamental units. For example, the unit of force is kg*m/s², which is known as the newton (denoted N).

Now you might be asking, “How do we find the damping force?”

The damping force always acts against velocity. This means the force takes on the form

μ is a nonnegative function of velocity. For some objects and for small velocities, the damping force is proportional to the velocity. This means that μ is a nonnegative constant, which is called the damping constant.

Some other examples for you (taken out of context of examples, but useful in many aspects):

Let’s now talk about the existence and uniqueness of second-order differential equations. They’re very similar to first-order. Also, just for your information, all of the theorems and propositions will be direct quotes from the book, since they explain them the best. Also, I’m going to use the theorem and proposition numbers they have in the book.

Theorem 1.17: “Suppose the functions p(t), q(t), and g(t) are continuous on the interval (α, β). Let t₀ be any point in (α, β). Then for any real numbers y₀ and y₁ there is one and only one function y(t) defined on (α, β), which is a solution to

and satisfies the initial conditions y(t₀) = y₀ and y^’(t₀) = y₁” (140).

The major difference between this theorem for second order differential equations and the related theorem for first order differential equations back in section 2.7 is that there is an initial condition needed for both the function y and the function y^’. Also note that this theorem can be sure a solution exists, and that it exists over the interval where the coefficients are defined and continuous.

Proposition 1.18: “Suppose that y₁ and y₂ are both solutions to the homogeneous, linear equation

Then the function

is also a solution to [this equation] for any constants C₁ and C₂” (141).

Here’s the proof for that:

Another definition for you: a linear combination of two functions u and v is a function of the form w= Au + Bv. A and B are just constants for this.

With this definition, our proposition can be stated by saying a linear combination of two solutions to a differential equation is also a solution to that differential equation.

Two functions u and v are linearly independent on an interval (α, β) if neither of them is a multiple of the other on that interval. If one is a constant multiple of the other on that interval, then they are said to be linearly dependent. For example, u(t) = t and v(t) = t² are linearly independent on the entire real plane (negative infinity to positive infinity). Linearly dependent functions would be u(t) = t and v(t) = 17t.

Theorem 1.23: “Suppose that y₁ and y₂ are linearly independent solutions to the equation

Then the general solution to [this equation] is

where C₁ and C₂ are arbitrary constants” (142).

Two linearly independent solutions, like the solutions in Theorem 1.23, form what is called a fundamental set of solutions.

So if we want to prove this theorem, we need to think about linear independence. Usually by simple observation, we can tell whether or not two functions are linearly independent. Sometimes that isn’t the case though. So we use something called the Wronskian. The Wronskian of two functions (let’s call them u and v) would be

You might be asking, “What does this tell us about anything?”

Here’s a proposition to answer this question for you.

Proposition 1.26 and 1.27 are about the results of the Wronskian and what that means for the homogenous differential equation. They are summed up in proposition 1.29, which I will quote for you now:

Proposition 1.29: “Suppose the functions u and v are solutions to the linear, homogeneous equation

in the interval (α, β). If W(t₀) ≠ 0 for some t₀ in the interval (α, β), then u and v are linearly independent in (α, β). On the other hand, if u and v are linearly independent in (α, β), then W(t) never vanishes in (α, β)” (144).

The proof of this proposition is the other two propositions that kind of work like exposition to this major proposition.

Tying everything back together, here’s the proof for Theorem 1.23:

One last thing to leave you with: When formulating initial value problems for second-order differential equations, we need to specify both a y(t₀) and a y^’(t₀). We had a theorem for that, but it applies to all second-order differential equations.

That’s all section 4.1 has to throw at you. I'll see you when I see you.

3.4, the bonus section of bonus sections

Bonus section!

Section 3.4 is entitled “Electrical Circuits.”

There are quite a few things you can put into a circuit, but for the sake of this section, only four of these are important: a voltage source, an inductor, a capacitor, and a resistor.

Very briefly, a voltage source (think battery or generator) supplies the voltage to the circuit. Voltage causes electrons to move through the circuit, and the rate at which these electrons flow is called current. A resistor limits the current. A capacitor stores charge. An inductor resists the change in current that passes through it.

If you want more information about this stuff, I recommend this website, although you could always go to Wikipedia: http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html

Here’s what a circuit with all four of these items looks like:

Well, this is what the book portrays these things as. You would think voltage would be labeled with a V (especially when you consider that energy is denoted as an E), but sometimes voltage is referred to as the electromotive force, or emf. So in this case, a voltage source is labeled with an E. Since the voltage can sometimes be variable (changing) instead of constant through the circuit, we will denote the voltage source as a function of time, E(t).

Also, let’s talk about units. The most efficient way of doing this is to combine everything into one nice-looking chart.

Item	Denoted with	Units	Units denoted with
Voltage Source	E	Volts	V
Current	I	Amperes (Amps)	A
Resistor	R	Ohms	Ω
Inductor	L	Henrys	H
Capacitor	C	Farads	F
Charge	Q	Coulombs	C

Perhaps the next thing you’re asking is, “How do we solve a circuit such as this one?”

My answer will be, “With physics, of course! [And differential equations. Those too.]”

In order to deal with a circuit such as this one, we need to have some handy laws and rules and equations to govern ourselves with. The book calls them component laws, and we’ll look at five of them.

1. Ohm’s Law: The drop across a resistor is proportional to the current.

2. Faraday’s Law: The voltage drop across an inductor is proportional to the rate of change of current.

3. Capacitance Law: The voltage drop across a capacitor is proportional to the charge on the capacitor.

4. Kirchhoff’s voltage law (KVL): The sum of the voltage drops around any closed loop is zero.

5. Kirchhoff’s current law (KCL): The sum of currents flowing into a junction equals the sum of the currents flowing out of that junction (the book says “the sum of currents flowing into any junction is zero” (129), which is equivalent).

I gave very simple explanations for beautiful physics equations. If you care, here’s some more information on them (I especially enjoy Faraday’s Law, but that’s just me).

Ohm’s Law: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/ohmlaw.html

Faraday’s Law: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/farlaw.html

Capacitance Law: http://www.facstaff.bucknell.edu/mastascu/elessonsHTML/LC/Capac1.htm (It’s under the section “Voltage-Current Relationships In Capacitors”)

Kirchhoff’s Laws: http://www.facstaff.bucknell.edu/mastascu/elessonshtml/Basic/Basic5Kv.html and http://www.facstaff.bucknell.edu/mastascu/elessonshtml/Basic/Basic4Ki.html

The beautiful thing about KVL is that means we can sum the voltage across our three items and the voltage source, and that resulting voltage will be zero.

The book has the opposite (meaning the voltage source voltage is negative and the other three are positive), and those are equivalent. When performing KVL, I tend to think of the circuit having a total positive voltage E that is coming from the voltage source (since no other item in our circuit will add any voltage into the circuit). Then I subtract the voltage that goes across each of the items in our circuit. You can do it the opposite way, but just make sure you keep track of which is negative and which is positive.

Something that helps with keeping track of signs is to sum all the voltages going across the items in your circuit and setting that equal to the total voltage coming from the voltage source.

We can rewrite the voltages going across our three items since we have handy laws for each of our three items. Thus

We defined current as the rate at which electrons (read: charge) flows. This means that I = dQ/dt and we can eliminate the Q from our equation. By differentiating each side of the equation, we get

Since this is a differential equation and this is a differential equations blog, we should set some initial conditions to make our lives easier. Usually, when we start off with a circuit, the charge on the capacitor is zero (meaning the capacitor is fully discharged) and the initial current is also zero. However, we still have a tricky second-order differential equation in our problem. We haven’t formally learned how to solve a second-order differential equation (spoiler alert: it’s going to be a thing in the future), so we’re going to save the second order-ness for a different time (perhaps our bonus section will make a brilliant comeback in the future).

If we just remove the capacitor from the circuit, then our equation becomes

Now this is something we can solve. It’s much easier when you already know the resistance and inductance of the circuit. It’s also much easier when the voltage is a constant rather than a function of time. In any event, I will leave you with this newfound knowledge of electrical circuits and bid you adieu until chapter 4.

3.3: Shall we save? (or withdraw. I don't really care what you do with your money.)

Section 3.3 is entitled “Personal Finance.”

Here’s another handy application for differential equations!

So P(t) will be the monetary balance at some time t of our bank account (how do you expect us to pay for our amoeba projects?). Our account will pay us some interest at a rate r per year, and this interest is compounded continuously. Between our time t and some change in t, which we will denote as Δt + t, would be P(Δt + t) – P(t) = interested earned in that time Δt. Since we originally denoted r as interest per year, this means that the interest earned over our change in time Δt is approximately (but not necessarily equal to) rPΔt.

So, like last section, we’ll take the derivative of our function P(t) by using the limit quotient definition of the derivative, which would make our differential equation P^’(t) = rP.

This is a differential equation that is easily separable and solvable (remember from some time ago, we called these types of differential equations exponential equations). Then our solution will have the form

Well, we should remind ourselves that this is real life, where we don’t just leave money in accounts forever and ever. I mean, we have amoebas to count. So let’s look at a savings account with a balance P(t) and we withdraw a balance W every year. There’s still an interest rate r that pays us interest every year (still compounded continuously). So our interest we earn will be similar to our first equation, but this time we add in the effect of withdrawals:

We’re going to make the same assumption like last time and say that the interest earned over this time is approximately rPΔt. However, we want to include something about the withdrawals. So we defined W as the money we withdraw per some time interval, so in a time Δt, we would withdraw WΔt. Rewriting our equation a bit, we would then have

Our derivative would now be rP – W, and thus this would be our model dP/dt. Conversely, if we deposit some amount of money D per year, our equation would be P^’ = rP + D.

There’s a paragraph about keeping track of the dimensions of the quantities (i.e. units). It’s just giving you reasons as to why we multiplied what we did to get the answers we did. As long as you keep track of units on each variable or constant, then you’ll be all good.

For the most part, this was all the new material in this section. I’m going to work through an example (since a majority of application problems and pretty much all of the problems you will come across for personal finance will be word problems). I don’t blame you, though, if you stop reading after this sentence.

Something else we do in real life is saving money for something important in our lives.  That might be for college. That might be for a house or a car. That might be for amoebas. (Okay, that was my last amoeba reference, I promise.)

Okay, just as an example, say we want to save for something that isn’t single-celled, so we want to put $1000 dollars in a savings account every year for 10 years. We start with nothing and we find a great %5 interest rate for our account. Very briefly we said that if we were to deposit money into an account and not withdraw anything, our equation would be P^’ = rP + D. Our r in this case would be 0.05 (since 5% is a percentage and all) and our D would be 1 (if we were to put our units in thousands of dollars). This would make our equation

Back in section 2.4, we said this is the form for a linear equation. Solving this is pretty simple, but I’ll summarize what we should do very quickly: find an integrating factor, multiply our equation by that integrating factor, integrate both sides and solve for P(t). Easy enough?

So our initial condition would be when P(0) = 0, since we started with nothing. This would make our C a positive 20, and then our final equation would be

That was pretty straightforward, right? As long as the differential equation isn’t too difficult to solve, then we’ll be golden.

We can add layers onto the personal finance application, by deciding how we’re going to save the money and where exactly that money will be coming from and when we’ll start to save that money. One of the examples, for instance, talks about a fixed percentage of our salary that we would deposit straight into our account and not touch. We could also add a layer of difficulty to that fixed percentage by making that an equation that would change as our salaries would increase (assuming our salaries increase when we work). In that case, we would be able to enjoy what little money we had at first and then save more as our salaries increased.

I guess the real moral of this section would be that life is hard and stuff is expensive and you have to save money to afford expensive stuff in the future. Now you can approximate how much money you have to save in order to afford expensive stuff! Yay differential equations!

By the way, this is the last section I have to summarize from this chapter. This is sad, considering the next section is about electrical circuits and this directly relates to my life. I'm quite ahead of the section my lecture is on, so I might just do electrical circuits because I would like to spread the physics love. 

In any event, I'll be seeing you something in the new future in chapter 4. Who knew time could fly so fast when we're having fun?